![Operating Systems: Three Easy Pieces [Concurrency Ch.4: Locked Data Structures]](https://cdn.hashnode.com/res/hashnode/image/upload/v1634310199364/TFaOr2-wP.jpeg?w=1600&h=840&fit=crop&crop=entropy&auto=compress,format&format=webp)
Operating Systems: Three Easy Pieces [Concurrency Ch.4: Locked Data Structures]
In this chapter we will see couple of famous data structures that we will convert them to be a concurrent data structure and at the end, we will see some tips when you develop your own concurrent data structure
You should always think about your locks in the data structure and putting them in the correct place as they can help in increasing the performance as we discussed in the previous chapter and we will see it more in this chapter
to start we should know that adding locks to a data structure to make it usable by threads makes the structure thread safe, exactly how such locks are added determines both the correctness and performance of the data structure.
so let's start with a simple example
Concurrent Counters
One of the simplest data structures is a counter. It is a structure that is commonly used and has a simple interface is Simple But Not Scalable, requiring a tiny amount of code to implement but how can we make this thread safe? basic code for counter data structure without locks
typedef struct __counter_t {
int value;
}
counter_t;
void init(counter_t * c) {
c - > value = 0;
}
void increment(counter_t * c) {
c - > value++;
}
void decrement(counter_t * c) {
c - > value--;
}
int get(counter_t * c) {
return c - > value;
}
you just need to add locks at critical sections and will be done At this point, you have a working concurrent data structure. The problem you might have is performance. If your data structure is too slow, you’ll have to do more than just add a single lock; such optimizations, Note that if the data structure is not too slow, you are done! the book is not going too deep about optimizations. we can make something like this with locks
typedef struct __counter_t {
int value;
pthread_mutex_t lock;
}
counter_t;
void init(counter_t * c) {
c - > value = 0;
Pthread_mutex_init( & c - > lock, NULL);
}
void increment(counter_t * c) {
Pthread_mutex_lock( & c - > lock);
c - > value++;
Pthread_mutex_unlock( & c - > lock);
}
void decrement(counter_t * c) {
Pthread_mutex_lock( & c - > lock);
c - > value--;
Pthread_mutex_unlock( & c - > lock);
}
int get(counter_t * c) {
Pthread_mutex_lock( & c - > lock);
int rc = c - > value;
Pthread_mutex_unlock( & c - > lock);
return rc;
}
Scalable Counting
The approximate counter works by representing a single logical counter via numerous local physical counters, one per CPU core, as well as a single global counter. Specifically, on a machine with four CPUs
there are four local counters and one global one. In addition to these counters, there are also locks: one for each local counter1 , and one for the global counter.
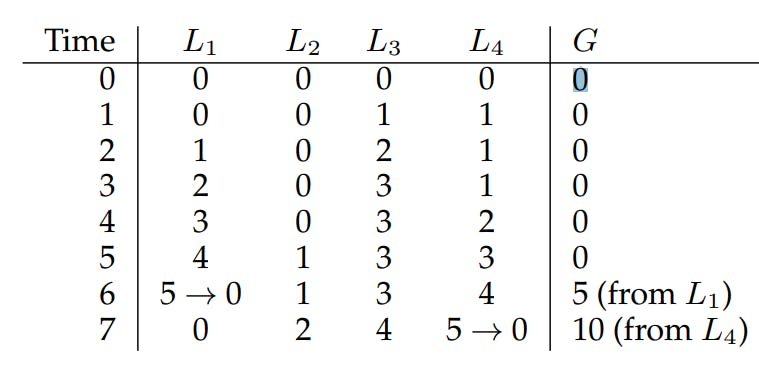
The basic idea of approximate counting is as follows. When a thread running on a given core wishes to increment the counter, it increments its local counter; access to this local counter is synchronized via the corresponding local lock. Because each CPU has its own local counter, threads across CPUs can update local counters without contention, and thus updates to the counter are scalable
However, to keep the global counter up to date (in case a thread wishes to read its value), the local values are periodically transferred to the global counter, by acquiring the global lock and incrementing it by the local counter’s value; the local counter is then reset to zero.
typedef struct __counter_t {
int global; // global count
pthread_mutex_t glock; // global lock
int local[NUMCPUS]; // per-CPU count
pthread_mutex_t llock[NUMCPUS]; // ... and locks
int threshold; // update frequency
}
counter_t;
// init: record threshold, init locks, init values
// of all local counts and global count
void init(counter_t * c, int threshold) {
c - > threshold = threshold;
c - > global = 0;
pthread_mutex_init( & c - > glock, NULL);
int i;
for (i = 0; i < NUMCPUS; i++) {
c - > local[i] = 0;
pthread_mutex_init( & c - > llock[i], NULL);
}
}
// update: usually, just grab local lock and update
// local amount; once local count has risen ’threshold’,
// grab global lock and transfer local values to it
void update(counter_t * c, int threadID, int amt) {
int cpu = threadID % NUMCPUS;
pthread_mutex_lock( & c - > llock[cpu]);
c - > local[cpu] += amt;
if (c - > local[cpu] >= c - > threshold) {
// transfer to global (assumes amt>0)
pthread_mutex_lock( & c - > glock);
c - > global += c - > local[cpu];
pthread_mutex_unlock( & c - > glock);
c - > local[cpu] = 0;
}
pthread_mutex_unlock( & c - > llock[cpu]);
}
// get: just return global amount (approximate)
int get(counter_t * c) {
pthread_mutex_lock( & c - > glock);
int val = c - > global;
pthread_mutex_unlock( & c - > glock);
return val; // only approximate!
}
the time taken to update the counter four million times on four processors is hardly higher than the time taken to update it one million times on one processor.
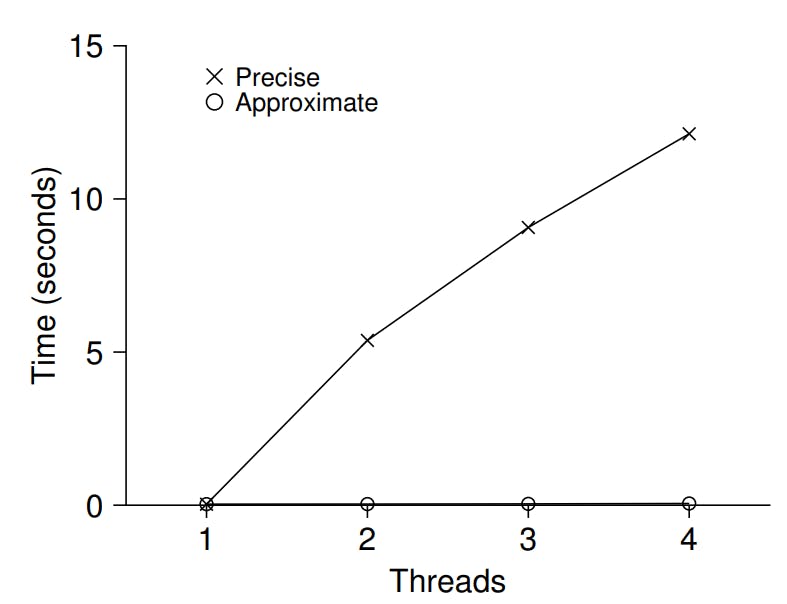
with four threads each incrementing the counter 1 million times on four CPUs. If S is low, performance is poor (but the global count is always quite accurate); if S is high, performance is excellent, but the global count lags (by at most the number of CPUs multiplied by S)
This accuracy/performance tradeoff is what approximate counters enable.
Concurrent Linked Lists
Let’s start with a basic approach once again. For simplicity, we’ll omit some of the obvious routines that such a list would have and just focus on concurrent insert; we’ll leave it to the reader to think about lookup, delete, and so forth
// basic node structure
typedef struct __node_t {
int key;
struct __node_t * next;
}
node_t;
// basic list structure (one used per list)
typedef struct __list_t {
node_t * head;
pthread_mutex_t lock;
}
list_t;
void List_Init(list_t * L) {
L - > head = NULL;
pthread_mutex_init( & L - > lock, NULL);
}
int List_Insert(list_t * L, int key) {
pthread_mutex_lock( & L - > lock);
node_t * new = malloc(sizeof(node_t));
if (new == NULL) {
perror("malloc");
pthread_mutex_unlock( & L - > lock);
return -1; // fail
}
new - > key = key;
new - > next = L - > head;
L - > head = new;
pthread_mutex_unlock( & L - > lock);
return 0; // success
}
int List_Lookup(list_t * L, int key) {
pthread_mutex_lock( & L - > lock);
node_t * curr = L - > head;
while (curr) {
if (curr - > key == key) {
pthread_mutex_unlock( & L - > lock);
return 0; // success
}
curr = curr - > next;
}
pthread_mutex_unlock( & L - > lock);
return -1; // failure
}
we can rearrange the code a bit so that the lock and release only surround the actual critical section in the insert code, and that a common exit path is used in the lookup code. The former works because part of the insert actually need not be locked; assuming that malloc() itself is thread-safe, each thread can call into it without worry of race conditions or other concurrency bugs. we need just lock in critical section only. As for the lookup routine, it is a simple code transformation to jump out of the main search loop to a single return path. Doing so again reduces the number of lock acquire/release points in the code.
void List_Init(list_t * L) {
L - > head = NULL;
pthread_mutex_init( & L - > lock, NULL);
}
void List_Insert(list_t * L, int key) {
// synchronization not needed
node_t * new = malloc(sizeof(node_t));
if (new == NULL) {
perror("malloc");
return;
}
new - > key = key;
// just lock critical section
pthread_mutex_lock( & L - > lock);
new - > next = L - > head;
L - > head = new;
pthread_mutex_unlock( & L - > lock);
}
int List_Lookup(list_t * L, int key) {
int rv = -1;
pthread_mutex_lock( & L - > lock);
node_t * curr = L - > head;
while (curr) {
if (curr - > key == key) {
rv = 0;
break;
}
curr = curr - > next;
}
pthread_mutex_unlock( & L - > lock);
return rv; // now both success and failure
}
Concurrent Queues
As you know by now, there is always a standard method to make a concurrent data structure: add a big lock. For a queue, we’ll skip that approach, assuming you can figure it out.
instead, we’ll take a look at a slightly more concurrent queue
typedef struct __node_t {
int value;
struct __node_t * next;
}
node_t;
typedef struct __queue_t {
node_t * head;
node_t * tail;
pthread_mutex_t head_lock, tail_lock;
}
queue_t;
void Queue_Init(queue_t * q) {
node_t * tmp = malloc(sizeof(node_t));
tmp - > next = NULL;
q - > head = q - > tail = tmp;
pthread_mutex_init( & q - > head_lock, NULL);
pthread_mutex_init( & q - > tail_lock, NULL);
}
void Queue_Enqueue(queue_t * q, int value) {
node_t * tmp = malloc(sizeof(node_t));
assert(tmp != NULL);
tmp - > value = value;
tmp - > next = NULL;
pthread_mutex_lock( & q - > tail_lock);
q - > tail - > next = tmp;
q - > tail = tmp;
pthread_mutex_unlock( & q - > tail_lock);
}
int Queue_Dequeue(queue_t * q, int * value) {
pthread_mutex_lock( & q - > head_lock);
node_t * tmp = q - > head;
node_t * new_head = tmp - > next;
if (new_head == NULL) {
pthread_mutex_unlock( & q - > head_lock);
return -1; // queue was empty
}
* value = new_head - > value;
q - > head = new_head;
pthread_mutex_unlock( & q - > head_lock);
free(tmp);
return 0;
}
there are two locks, one for the head of the queue, and one for the tail. The goal of these two locks is to enable concurrency of enqueue and dequeue operations. In the common case, the enqueue routine will only access the tail lock, and dequeue only the head lock. One trick is to add a dummy node (allocated in the queue initialization code); this dummy enables the separation of head and tail operations.
in next chapter ( condition variables) we will discuss another way to write queue which will be more practical.
Concurrent Hash Table
This concurrent hash table is straightforward, is built using the concurrent lists we developed earlier, and works incredibly well.
#define BUCKETS(101)
typedef struct __hash_t {
list_t lists[BUCKETS];
}
hash_t;
void Hash_Init(hash_t * H) {
int i;
for (i = 0; i < BUCKETS; i++)
List_Init( & H - > lists[i]);
}
int Hash_Insert(hash_t * H, int key) {
return List_Insert( & H - > lists[key % BUCKETS], key);
}
int Hash_Lookup(hash_t * H, int key) {
return List_Lookup( & H - > lists[key % BUCKETS], key);
}
The reason for its good performance is that instead of having a single lock for the entire structure, it uses a lock per hash bucket (each of which is represented by a list). Doing so enables many concurrent operations to take place. this simple concurrent hash table scales magnificently; the linked list, in contrast, does not.
Summary
The best practise when you develop your own concurrent data structure is to avoid premature optimization (knuth’s law)
When building a concurrent data structure, start with the most basic approach, which is to add a single big lock to provide synchronized access. By doing so, you are likely to build a correct lock; if you then find that it suffers from performance problems, you can refine it, thus only making it fast if need be. We can ended by famous quote “Premature optimization is the root of all evil.”